First steps on 3D reconstruction

I started by trying to build an entire pipeline to see the end results of the 3D points. This way it is easier to see if something is going wrong in one of the steps.

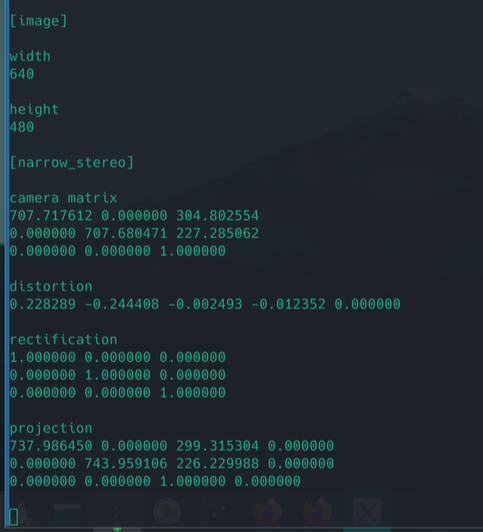
I tried to retrieve the intrinsic parameters of my smartphone’s camera from the image’s metadata, but I was getting weird results. Then I tried to get them manually, but someone in the lab reminded me that smartphones have auto-focus and the parameters change. To avoid messing with my phone, I simply used another camera that was available and not being used by anyone in the lab (an Orbbec Astra Pro) and got the intrinsic parameters using a chessboard and a ROS tool

I used SIFT once more to get the matching points from two viewpoints:

Then, found the Essential matrix → Rotation and Translation → Projection matrices

With the matching points and projection matrices, I triangulated and plotted the points (ignoring the distortion parameters) and got this:

But the Essential matrix is defined only up to scale (in the illustration it is the fundamental matrix, but the essential matrix comes from the fundamental matrix knowing the intrinsic parameters).

OpenCV has a function that solves this by setting the distance between cameras to 1, which means that the distance between points is relative to the distance between cameras. We can retrieve the real scale factor by having an object in the image of known dimensions.

Using the distortion factors, I got weird results and I haven’t found out yet what I did wrong:

Re-calibrating the camera with more images and still ignoring the distortion parameters, the results are apparently better

Then I experimented with bending the paper like this:

With SIFT I got this:

And plotting, I got this:

This result gave me more confidence about the reliability of the previous steps.

Then, I started working on a 3D reconstruction of the object. I started by trying some OpenCV functions. The functions that I found create disparity maps, and the goal was to create a 3D plot from those maps. With this approach, I only got bad results without any meaning, and I gave up.

Using the two images from the two viewpoints and doing the dot product between the fundamental matrix and the coordinates of the pixel in analyses in the first image, the result is a vector containing the $a$, $b$, and $c$ parameters of the epipolar line ($ax + by + c = 0$) in the second image:

Inside the epipolar line will be the point of image 2 that matches the point in analyses of image 1. This reduces the search of the matching point by a lot, being a 1D search instead of a 2D search.

Although the search is less than without the epipolar line, there are many points, and even using the simplest algorithm possible to compare the windows of pixels (absolute distance between arrays—cv2.norm()) from the two images, the time of execution using Python is more than 10 minutes.

The cv2.norm() is not ideal for this use case and generates a lot of errors, but by removing isolated points, I got this:

After that, I decided to try to optimize the code, but I only got minor improvements. So, I took a C++ course and implemented the slowest function in C++. The major part of the program is written in Python, and the function with high computation cost is written in C++ and compiled. With this, the computation time of the function is less than 30 seconds, more than 30x faster than Python.

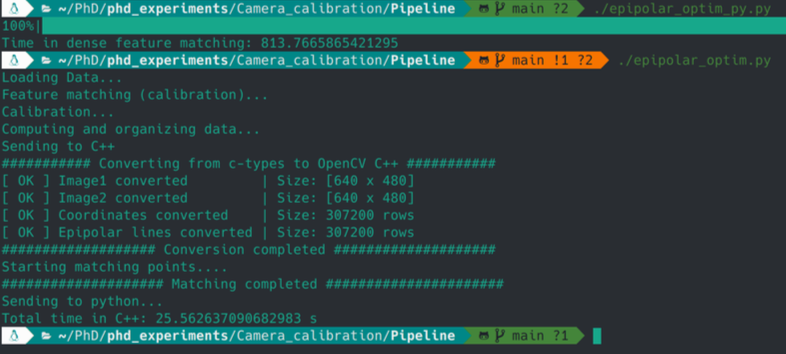
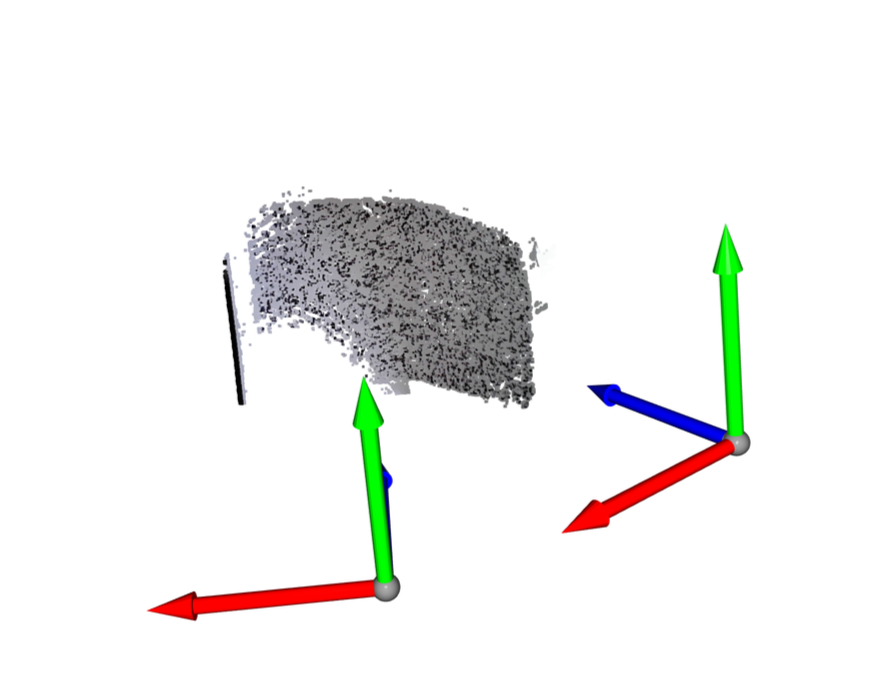
The current pipeline looks like this:

Unanswered questions:

• What are the best algorithms (green boxes) for the current pipeline?
• How can I evaluate the quality of the results?
• How can I estimate the intrinsic parameters after changing the focal length?
• In a stream of images (after motion scope), should I rerun the current pipeline each time, or should I use some kind of tracking algorithm?